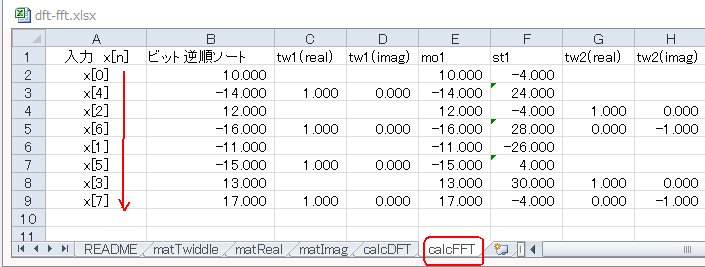
4-01　DFTとFFT〜乗算の数を比較してみよう（続き） ●最後のシートでに８点FFTを計算する 　FFT(高速フーリエ変換、Fast Fourier Transform)では乗算の数を大幅に減らすことができます。 　calcFFTシートではまず入力 x[n] を図4‐08のように n = 0, 4, 2, 6, 1, 5, 3, 7 と並び替えます（元々はこの図のA列の並び）。 　　図4-08　入力データの並びに注意 ●並び替えには規則性がある 　この並び替えは「ビット逆順ソート」と呼ばれ、表4‐02のような規則で x[n] を並び替えます（＊１）。 （＊１）もし x[n] がRAMに格納されている場合はアドレスビットの上〜下位を逆にして読み出せばよい。 元の順序 2進数にする ビット逆順 FFTでの順序 0 000 000 0 1 001 100 4 2 010 010 2 3 011 110 6 4 100 001 1 5 101 101 5 6 110 011 3 7 111 111 7 　　表4-02　この規則でx[n]を並び替え ●FFT演算シートの各列の説明 　calcFFTシートの下の方に「フロー」と「各列」の対応図があります（図4‐09）。 　例えばtw1は「ステージ1」の回転因子で4つとも右向き、すなわち複素数では"1+j 0"になり（これ参照）、図4‐08のtw1列もそのようになっています(real=1, imag=0)。 　mo1はx[n]に回転因子を掛けた結果になりますが、4つの回転因子は"1+j 0"すなわち"1"です。図4‐08のmo1列を見ると、x[n]がそのまま転写されています。 　mo1の値を足したり引いたりしたものがst1、これがステージ1の結果になります。図4‐08のst1列にそれらの値があります。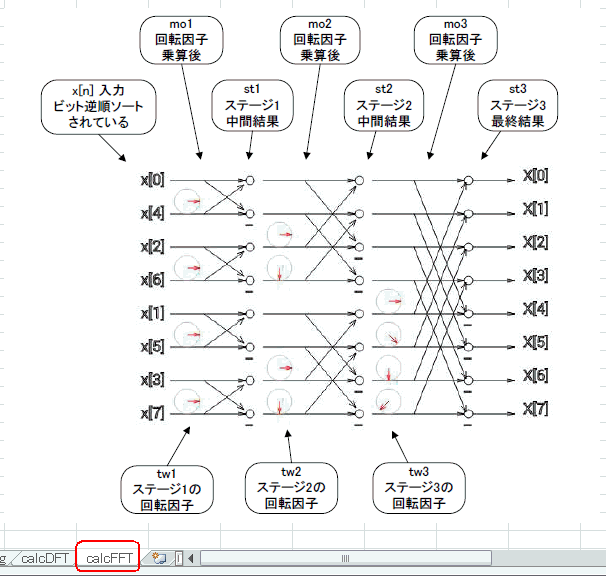 　　図4-09　フローと各列の対応図 ●ステージ２の結果は複素数になる 　tw2は「ステージ2」の回転因子です。図4‐09では右向きと下向きがあり、図4‐10のtw2列(real/imag)では"1+j 0", "0-j 1"となっています（これ参照）。 　ステージ2の入力はst1、それにtw2をかけたものがmo2になります。回転因子が虚数部を含むことにより、mo2列は(real/imag)に分かれ、図4‐10のようになります（各セルをクリックすると計算式が見れる）。 　フローに沿って演算を進めるとステージ2の結果は図4‐10のst2列(real/imag)のようになります。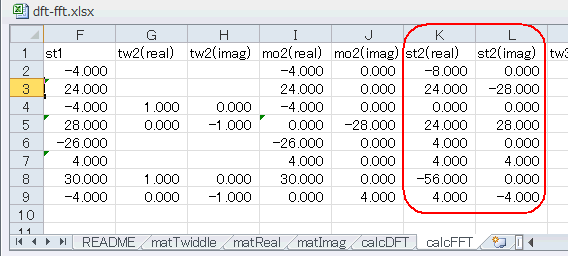 　　図4-10　ステージ１の結果は実数、ステージ２の結果は複素数 ●ステージ３の結果が８点FFTの結果になる 　tw3は「ステージ3」の回転因子です。図4‐09を見ると右向き、下向きに加え、斜め右下向き、左下向きがあります。図4‐11のtw3列(real/imag)には"0.707-j 0.707", "-0.707-j 0.707"が見られます（これ参照）。 　ステージ3の入力はst2、それにtw3をかけたものがmo3になります。入力、回転因子ともに虚数部を含むことから、mo3列(real/imag)の計算はやや複雑になります（各セルをクリックすると計算式が見れる）。 　フローに沿って演算を進めるとステージ3の結果は図4‐11のst3列(real/imag)のようになります。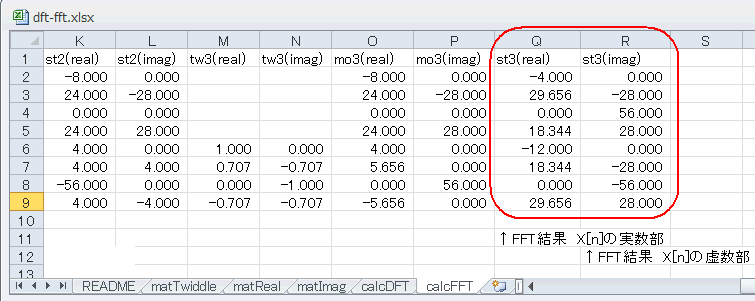 　　図4-11　calcFFTの右端に８点FFTの結果 ●FFTとDFTは結局同じことなので・・・ 　ひるがえってDFTの結果（図4‐12）を見ると、FFTの結果（図4‐11）と一致していることが分かります（演算時の切り捨ての関係で小数点以下の値は微妙に違う）。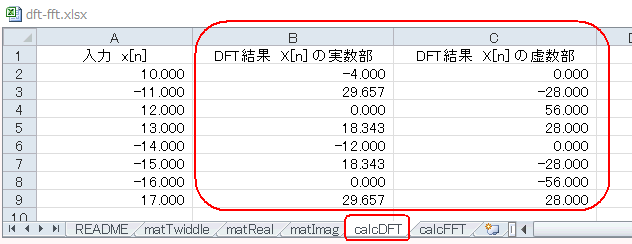 　　図4-12　前のシート（calcDFT）を見る ●各セルをクリックして乗算（＊）を数えてみる 　それでは乗算数を数えてみましょう。mo2列(real/imag)で計4回、mo3列(real/imag)で計12回、合計16回の乗算が行われています（図4‐13、各セルをクリックすると計算式が見れる）。 　DFTが128回だったことを鑑みると大幅に減っていることが分かります。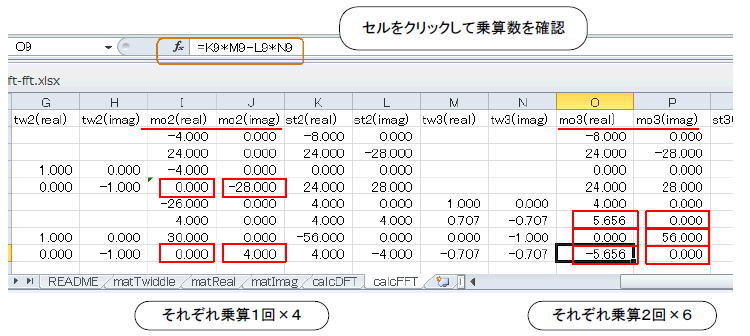 　　図4-13　赤枠のセルで乗算が行われている ●点数が多いと N -> log2(N) の違いが効いてくる 　このフローを見てわかるようにFFTの場合、複素乗算数は (N/2)*log2(N) になります。DFTはN*N なので、Nの数が増えるにつれてその差は著しく広がります（＊１）。 （＊１）N=4096の場合 -> log2(4096)=12 なので300倍以上速くなる可能性がある。 　FFTは点数が2の累乗という制限がありますが、高速化効果がこのように強大です。現状ではDFTは限定的に使われ、ほとんどのケースでFFTが使われます。 最初のページへ 目次へ戻る