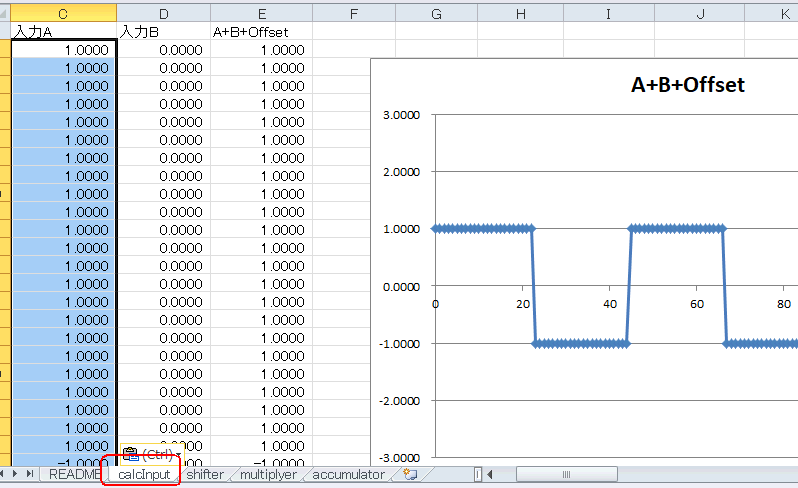
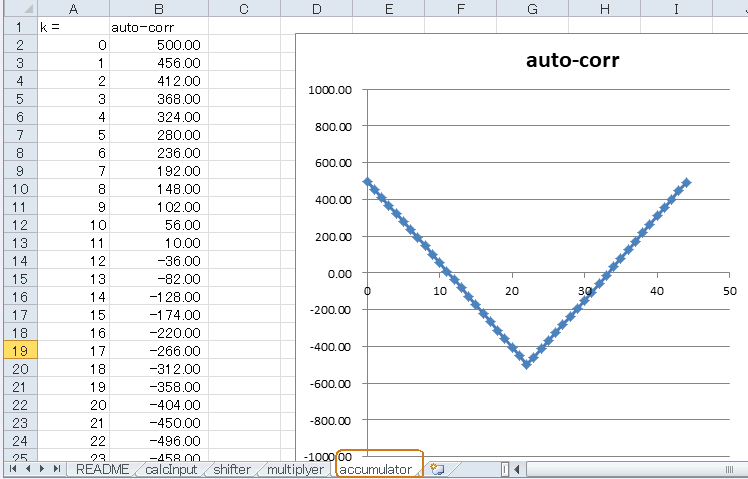
5-02　色々な周波数の自己相関を見る（続き） ●矩形波（台形波）を入力すると・・・ 　サイン波以外を入力するとどうでしょうか？これをコピーしてcalcInputシートにペーストします。図5‐26のように1kHzの矩形波になります。 　　図5-26　+1.0と-1.0を繰り返す矩形波 ●基本的な傾向としてはサイン波のときと同じ 　accumulatorシートを見ると図5‐27のように直線的な自己相関値になっています。矩形波とはいえ1kHzなのでサイン波の場合と同じく45サンプルで1周しています。 　　図5-27　k=22で極小、k=44で極大 ●三角波だとどうなるか 　次はこれをコピペしてみましょう。図5‐28のように1kHzの三角波になります。 　　図5-28　矩形波より形がサイン波に近い三角波 ●サイン波の場合と同じような自己相関値 　accumulatorシートを見ると図5‐29のように45サンプルで1周しています。矩形波と比べると三角波はボリュームが小さいので、いくらか振幅が減ります。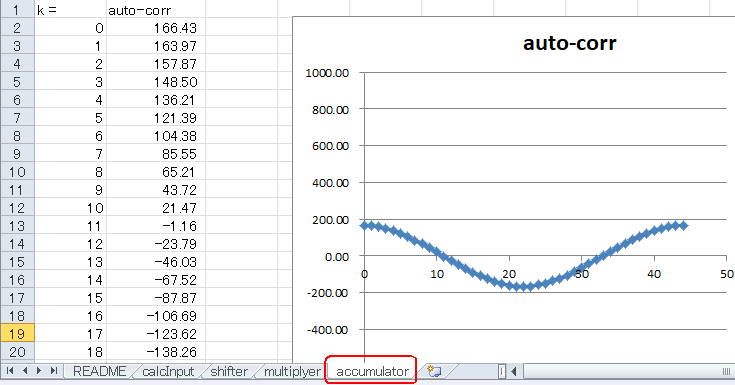 　　図5-29　三角波の自己相関値 ●のこぎり波の場合 　次はのこぎり波を入力してみましょう（これをコピペ）。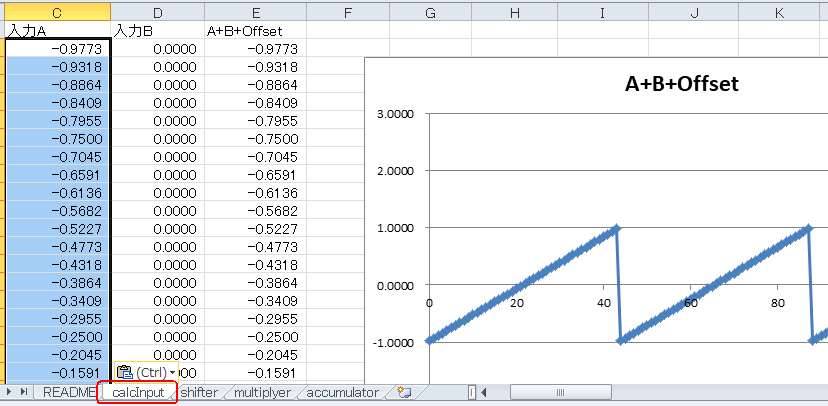 　　図5-30　のこぎり波（sawtooth-wave） ●やはり45サンプルで1周する 　自己相関値は図5‐31のようになります。1kHzの周期信号であることに変わりはないので、45サンプルで1周します。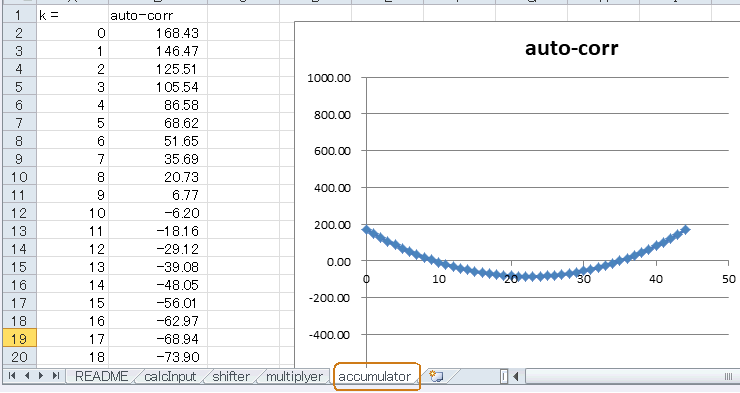 　　図5-31　のこぎり波の自己相関値 ●相関のない信号−ホワイトノイズ 　全く周期性のない信号はこれです。コピペしてみると図5‐31のような「白色雑音」になります。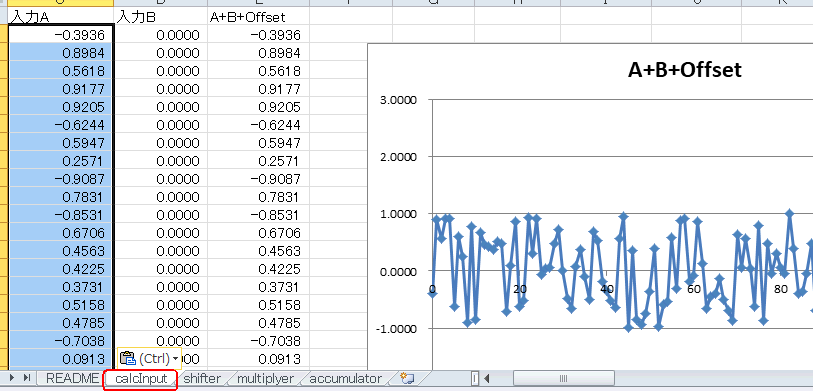 　　図5-32　音を聞くと「ザーーー」と聞こえる白色雑音 ●「自己相関がない」という結果になる 　自己相関値は図5‐33のようになります。k = 0だけは例外的に大きくなりますが、他は小さな値です。周期信号を含まないとこのような形になります。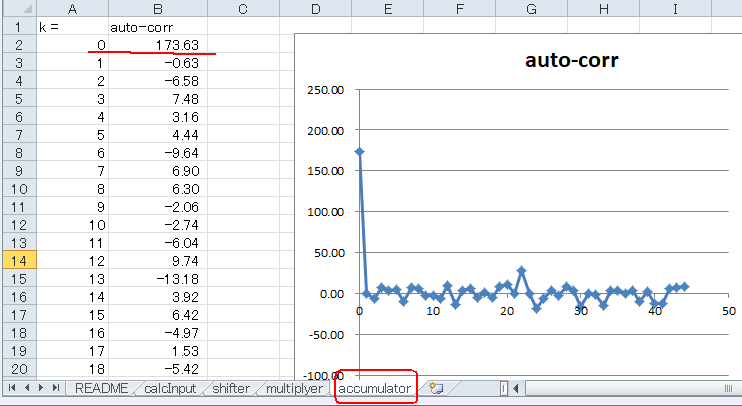 　　図5-33　正と負が揃ったり逆になったりしないのでこうなる ●きれいなサイン波でなくても周期性を発見できる 　矩形波、三角波、のこぎり波でも周期信号であれば、自己相関の「山と谷の位置」、「山と谷の差」でその周期性を解析できます。 　そして白色雑音のように周期信号でなければ、自己相関値にそのような山／谷は現れません。 最初のページへ 目次へ戻る